
 |
|
#1
|
|||
|
|||
|
Küçük Her Zaman Güzeldir: Sonsuz Küçükler
 Sonsuzun zıttı nedir diye sorsak, arası matematik ile fazla ilgili olmayan biri sıfır cevabını verebilir. Ancak elbette aradığımız cevap sıfır değildir. Sorduğumuz sorunun cevabı sıfırdan çok ama çok az daha büyük ama diğer bütün sayılardan küçük bir sayı olmalıdır. İşte bu büyüklük matematikte sonsuz küçük (infinitesimal) olarak tanımlanır. Sonsuz küçükler, ölçülemeyecek kadar küçük cisimleri tarif etmek için kullanılır. Sonsuz küçüklerden yararlanmaktaki asıl amaç nicelik bakımından çok küçük olsalar da hala açı, eğim gibi belirli özelliklere sahip olmalarıdır. Ancak buraya dikkat edelim. Aynen sonsuzluk gibi sonsuz küçüklerde aslında gerçek bir sayı değildir. Şöyle düşünelim. İki sayı aldığımız zaman bu iki sayının arasında her zaman bir başka sayının var olacağını biliriz. Bu mantıkla 0 ile 1 sayısının arasına istediğimiz kadar reel sayı sığdırabiliriz. Bu sayılardan biri 0.00000000000000001 olabilir. Bu sayı size sonsuz küçük gibi görünse de, yeni bir sonsuz küçük elde etmek için onu 10’a bölmeniz yeterlidir. Dolayısıyla, sonsuz gibi sonsuz küçük de yalnızca soyutlamada var olur. Sonsuz Küçükler Hesabı Nasıl Yapılır? Şimdi aşağıdaki örneğe bakalım. Dairenin alanını, içine çizilen üçgenlerin alanı yardımı ile toplamaya çalışalım. İlk dairemizi dört üçgene böldük. Ancak görselde de görebileceğiniz gibi dairenin içinde önemli bir miktar boşluk kaldı. Bu nedenle bu üçgenlerin alanlarının toplamı dairenin alanına eşittir diyemez. Bu hatayı azaltmak için daha fazla üçgen oluşturmaya çalışabiliriz. Evet, bu biçimde hata azalır ancak sonucumuz yine de hatalıdır.  Bu hatayı tamamen ortadan kaldırmak için onu sonsuz sayıda üçgene bölmemiz gerekir. işte bu noktada sonsuz sayıda üçgenin, sonsuz sayıda tabanı hemen hemen dairenin çevresini kaplayacaktır. Bu tabanlarımız artık o kadar küçüktür ki aradaki eğrilik neredeyse yok olmuştur. İşte bu sonsuz küçükler fikrine güzel bir örnektir. Şimdi devam edelim. Aşağıda soldaki şekli biraz bozalım. Sonuçta elimizde aynı alana sahip sonsuz sayıda üçgenimiz var. Bu üçgenleri kesip, tek bir noktada birleştirdiğimizi düşünelim. Gördüğünüz gibi yeni üçgenimizin tabanı aslında çemberin çevresine neredeyse eşittir. Bu sayede de bir dairenin alanını neredeyse bulmak mümkündür. Teoride bu cevap doğrudur ancak pratikte yine hatalıdır.  Bu hesaplamanın doğru olması için tabanın sonsuz küçük olması gerekir. Ancak ne kadar ince üçgen çizersek çizelim aslında daha da küçüğünün çizilebileceğini biliyoruz. Bu sonuç bir matematikçiyi rahatsız etse de, yani yukardaki neredeyse cümlesinden çok hoşlanmasak da, çoğunluk bunu görmezden gelir. Çünkü gördüğümüz gibi, elde edilen sonuçlar yanlış değildir. İşte bu nedenle sonsuz küçükler hesabı uzun bir süre matematikçileri ikiye ayırmıştır. Kepler’in Hacim Hesaplamaları Gökbilimci Johannes Kepler’i genellikle gezegenler ile ilgili çalışmaları ile tanırız. Ancak aslında kendisinin matematiğe de büyük katkıları bulunmuştur. Bunlardan bir tanesi de 1615’te, variller gibi kavisli şekillere sahip katıların hacimlerini hesaplamanın bir yolunu bulmasıydı. Bunu da aslında yukarıda aktardığımız sürece benzer bir biçimde yapmıştı. Kepler, bir fıçının veya herhangi bir 3 boyutlu şeklin hacmini bulmak için onu ince katmanlardan oluşan bir yığın olarak hayal etti. Toplam hacmi bulmak için yapmamız gereken şey, tüm katmanların hacimlerini toplamaktı. Kepler’in çözümü, sonsuz küçükler kavramını kabul ettiği için doğruydu. 1615’te sonuçlarını Nova stereometria doliorum vinariorum’da (Şarap fıçılarının yeni katı geometrisi) adlı kitabında yayınladı. Kepler bu çalışması ile 17. yüzyılda Isaac Newton ve Gottfried Leibniz tarafından kalkülüsün geliştirilmesinin yolunu açtı.  Johannes Kepler’in (1571-1630), alanları ve hacimleri hesaplamaya olan ilgisi, 1613’te Avusturya’nın Linz kentinde ikinci kez evlendiğinde meydana gelen bir olaydan kaynaklandı. Kepler düğün için bir fıçı şarap satın aldı. Ancak satıcının fıçının hacmini ölçme yönteminden pek memnun kalmadı. Bu, Kepler’e konu hakkında bir kitap yazması için ilham verdi. Bu çalışması daha sonra da integral hesabına ilham kaynağı olacaktı. Sonsuz Küçükler Ve İntegral Hesabı Hepinizin de bildiği gibi Leibniz ve Newton tarafından birbirinden bağımsız olarak keşfedilen Kalkülüs sonsuz küçükler hesabı üzerine kurulmuştur. Bir fonksiyonun integralini hesaplamaya kalktığımız zaman, esasen fonksiyona karşılık gelen eğrinin altındaki alanı hesaplarız. Ancak, yukarıda bir dairenin alanını hesaplama örneğinde anlattığımız gibi, bunu eğriyi sonsuz derecede küçük tabana sahip dikdörtgenlere bölerek yaparız. Dikdörtgenler ne kadar ince olursa, hata payı da o kadar küçük olur. 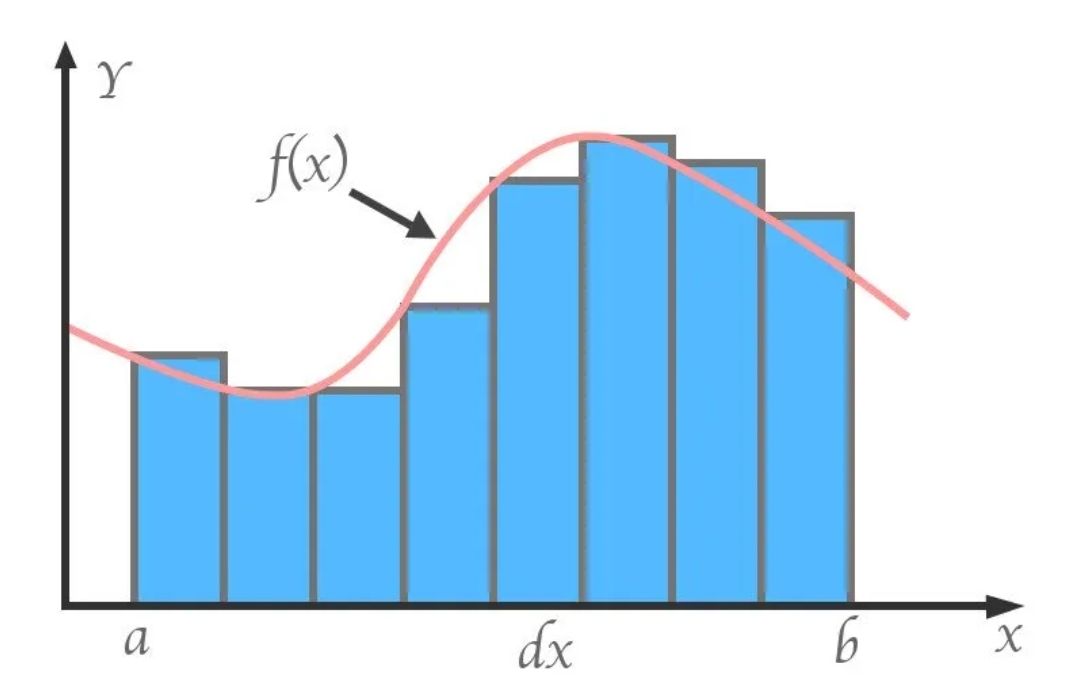 Burada ‘dx’ dediğimiz sonsuz küçük birimdir. Bir dikdörtgenin alanı iki dik kenarının birbiri ile çarpımıdır. Bu mantıkla yapmamız gereken şey az önceki örneklerde de gördüğümüz gibi her dikdörtgenin alanını hesaplamak ve sonra da bunları toplamaktır. Elbette ne kadar çok dikdörtgenimiz olursa o kadar cevaba yaklaşırız. Kalkülüs son 400 yıldaki en önemli matematiksel keşif olarak kabul edilir. Fizik ve mühendislikteki pek çok gelişme değişimin matematiği olarak da bilinen kalkülüs ile bir biçimde ilişkilidir. Bu, dikkatli bir gözlem ve sonsuz küçükler hesabı sayesinde mümkün olabilmiştir. |
|
#2
|
|||
|
|||
|
Güzel konu. İşlenişi de güzel. Uzun cümleler, girizgahlar ve tekrarlar yok, kolayca okunuyor.
|
|
#3
|
|||
|
|||
|
yazıda anlatılan Keplerin hesaplaması ve Newton ve Leibnize ilham vermiş olabiliyor olmasından hareketle Matematik tarihi yada matematiğin tarihsel gelişimi güzel bir kitap konusu olabilir. Oradaki zihinsel süreçler , alınan ilhamlar , belkide vardır bilemiyorum bu tarzda güzel kitaplar.
. |
|
#4
|
|||
|
|||
|
Sonsuzun zitti yine bir sonsuzdur...daha doğrusu sınırsızdir.
|
|
#5
|
|||
|
|||
|
İdealizm-Realizim ikilemi
Sonsuz büyük ve sonsuz küçük idealizmdir. Şu an ölçülebilir veya gelecekte ölçebileceğimiz en büyük ve en küçük ise realizmdir. |
|
#6
|
||||
|
||||
|
sonsuz sınırsızdır... sonsuzun tersi düzü başı sonu olmaz... üzerine koyacağınız her rakam ona sınır koyma çabasıdır... insan beyni bu kavramı algılayamaz bu nedenle ürker hemen ilahi güçü devreye sokma eğilimi başgösterir... sonsuzluğu ya da hiçliği tarife çalışmak bu yorum da dahil komik sonuçlara neden olur...

|
|
#7
|
||||
|
||||
|
Sonsuzun zıttı Sonlu dur .
Ucgenleri nekadar küçültürsen küçült , sonu bir yerde gelir, alan kalmayınca |
 |
|
|
 Benzer Konular
Benzer Konular
|
||||
| Konu | Konuyu Başlatan | Forum | Cevap | Son Mesaj |
| Polifenol nedir? Mideye faydası nedir? | Lady | Alternatif Tıp ve Bitkiler | 0 | 03.03.22 18:01 |
| Aşkın hakikati nedir, aşk nedir? | Torlak | Tasavvuf Sohbetleri | 1 | 07.10.21 16:17 |
| Avam nedir? Havas nedir? Bişey bilmeyen ben gibiler nedir? | Kgumus | Sorularınız | 30 | 04.07.21 18:41 |
| Varlık Nedir? Ruh Ölümlü müdür? Metafizik Nedir ?? | Och | Metafizik | 8 | 17.12.20 09:53 |
| Karabasan nedir? Uyku Felci tıbbi ve bilimsel olarak nedir? | SiLence | Gizemli Olaylar ve Mekanlar | 4 | 25.09.19 17:00 |